The purpose I write this blog

Mechanistic Interpretability is a new field in machine learning that aims to reverse engineering complicated model structures to something clear, understandable and hopefully controllable for our humans. The study of this field is still at a young age and facing mountains of challenges. While for beginners (like me), there are lots of terms or ideas which are not so familiar (e.g. superposition, circuits, activation patching, etc). Thus it’s a little bit difficult for people new to this area to figure out what researchers are really doing.

Therefore I write this blog to give a brief introduction to mechanistic interpretability without so much of horrible concepts. The blog aims to help you understand the basic ideas, main directions and latest achievements of this field, providing a list of resources to help you get started at the same time!

If you really want to do some cool research as a beginner, I highly recommend the guide by Neel Nanda.

What is Mechanistic interpretability?

Speaking of AI research, neural network is the tool that is used most widely nowadays for its excellent representation and generalization ability. What does a neural network do? It receives an input and gives an output after some calculations. Specifically speaking, it usually gets the representations of an input and maps it to an expected output under a predefined computation graph. From my perspective, neural networks mainly care about two things: create representations to extract features and establish the relationship between the representations and the output.

Why is neural network so popular? An important reason is that the neural network can save a lot of time for researchers to manually design features. For example, for natural language processing (NLP) people often designed features like “the frequency of a word that appears” or “the co-occurrence probabilities” in the past. Manually designing features caused too much labor, so people choose to use neural networks to find features automatically. As for optimizing, they set a goal of minimizing the loss function and using backward propagation (BP) to update the parameters of the model. Thus neural networks free our hands and improve performance at the same time.

All is well, so why do we concern about interpretability? Though neural networks can extract a lot of features with a high efficiency, we cannot have a clear understanding of what the features really are. For example, we know that a filter with Laplacian operator can extract the edge of an image, but we don’t know what the features extracted by a convolution layer mean because the parameters of the filters inside are often randomly initialized and optimized using BP algorithm. As a result, features in neural networks are often ambiguous.

Why is interpretability important? Actually this statement is controversial because some people say interpretability is bullshit💩. I’m not angry about this. Anyway, people’s taste varies, just like many people enjoy Picasso’s abstract paintings while I don’t. Interpretability still lacks exploring so it’s now far from application, and that’s why some people look down on it. While it is this lack of exploration that excites me most because there are a lot of unknown things waiting for me to discover! Actually, Interpretability is a key component in the AI alignment cycle (see Figure 0). The goal of alignment is to “make AI systems behave in line with human intentions and values” and interpretability plays an important role in ensuring AI safety. For example, unwanted things like malicious text generated by a language model may be avoided using model steering (a trick played on the activations during the forward propagation). Besides, having a clear understanding of neural networks enables us to focus on the relevant part of a model to a specific task and perform fine-tuning in a more precise way (haha here is an ad for my project: circuit-tuning).

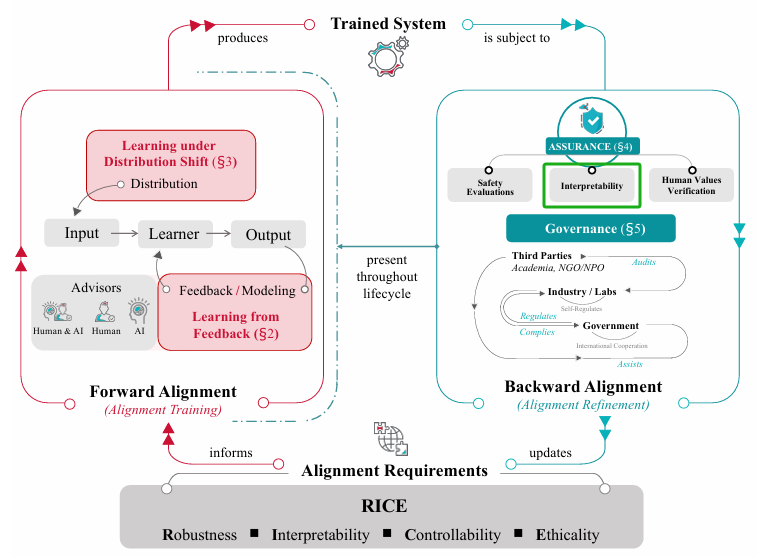Figure 0: The position of interpretability in the AI alignment cycle (from this survey)

Last question: what is mechanistic interpretability? Let’s call it mech interp first because I’m really tired of typing the full name💦. There seems not to be a rigorous definition, but I here I want to quote the explanation by Chris Olah:

  Mechanistic interpretability seeks to reverse engineer neural networks, similar to how one might reverse engineer a compiled binary computer program.

Another thing: there are various of categories of interpretability, such as studies from the geometry perspective or from the game theory and symbol system perspective, which can be found at ICML, ICLR, NeurlPS, etc. When we say mech interp, we often refer to the studies on Transformer-based generative language models now (though the research started before 2017) which will be introduced briefly in the next section. So before we start, let’s briefly go over the structure of Transformer first!

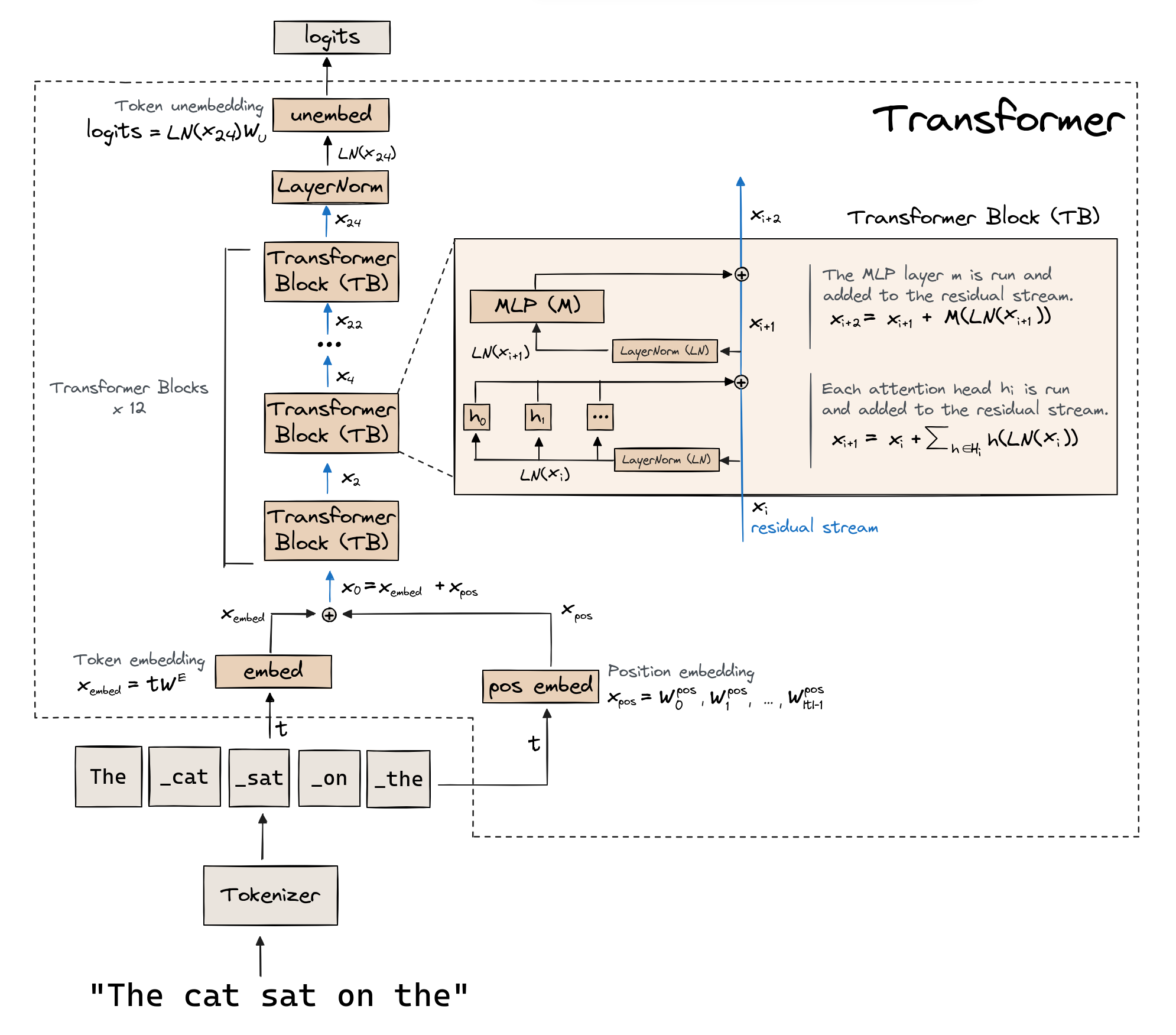Figure 1: The structure of Transformer (from Arena)

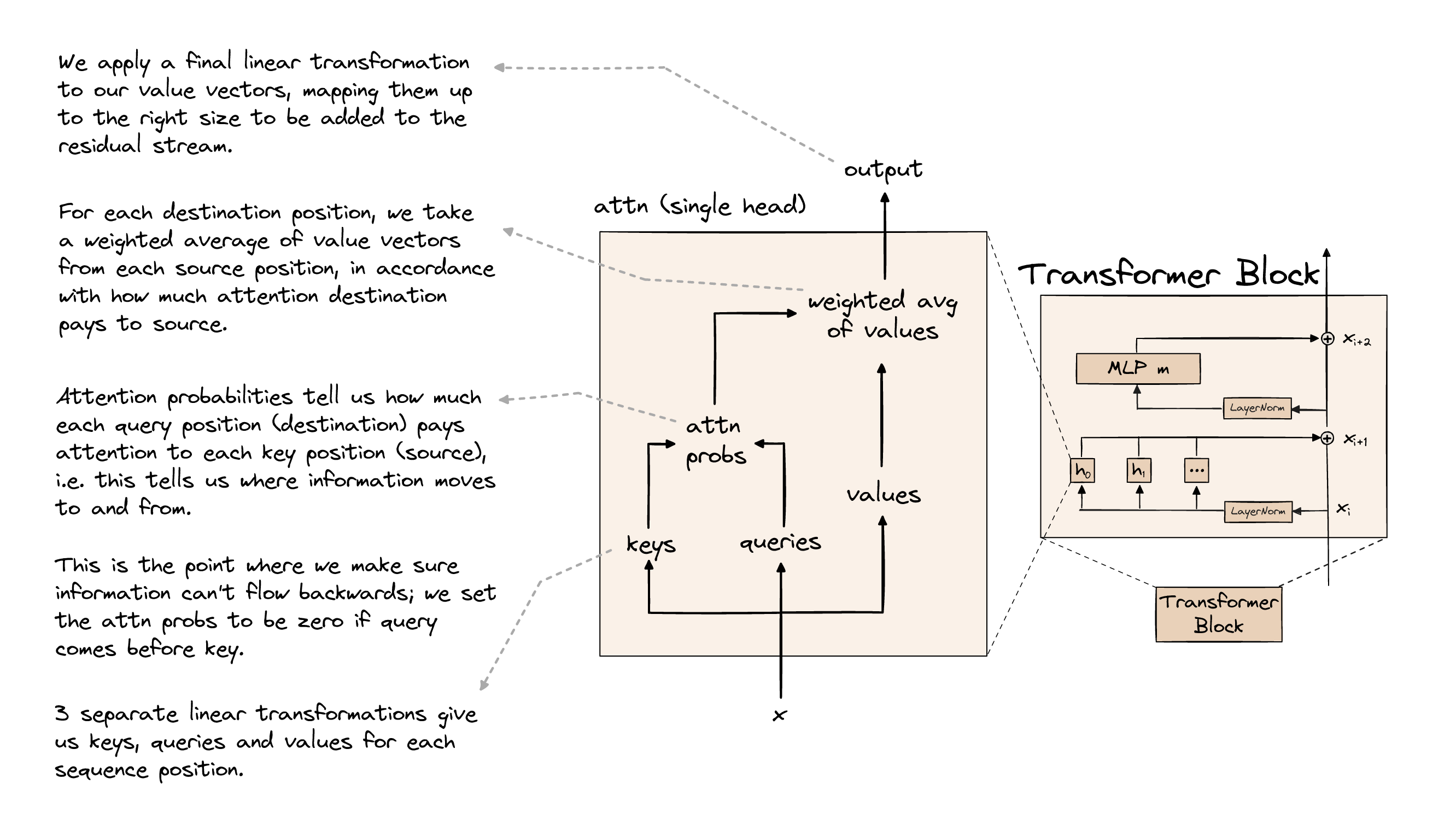Figure 2: The structure of the self-attention block in a Transformer block (from Arena)

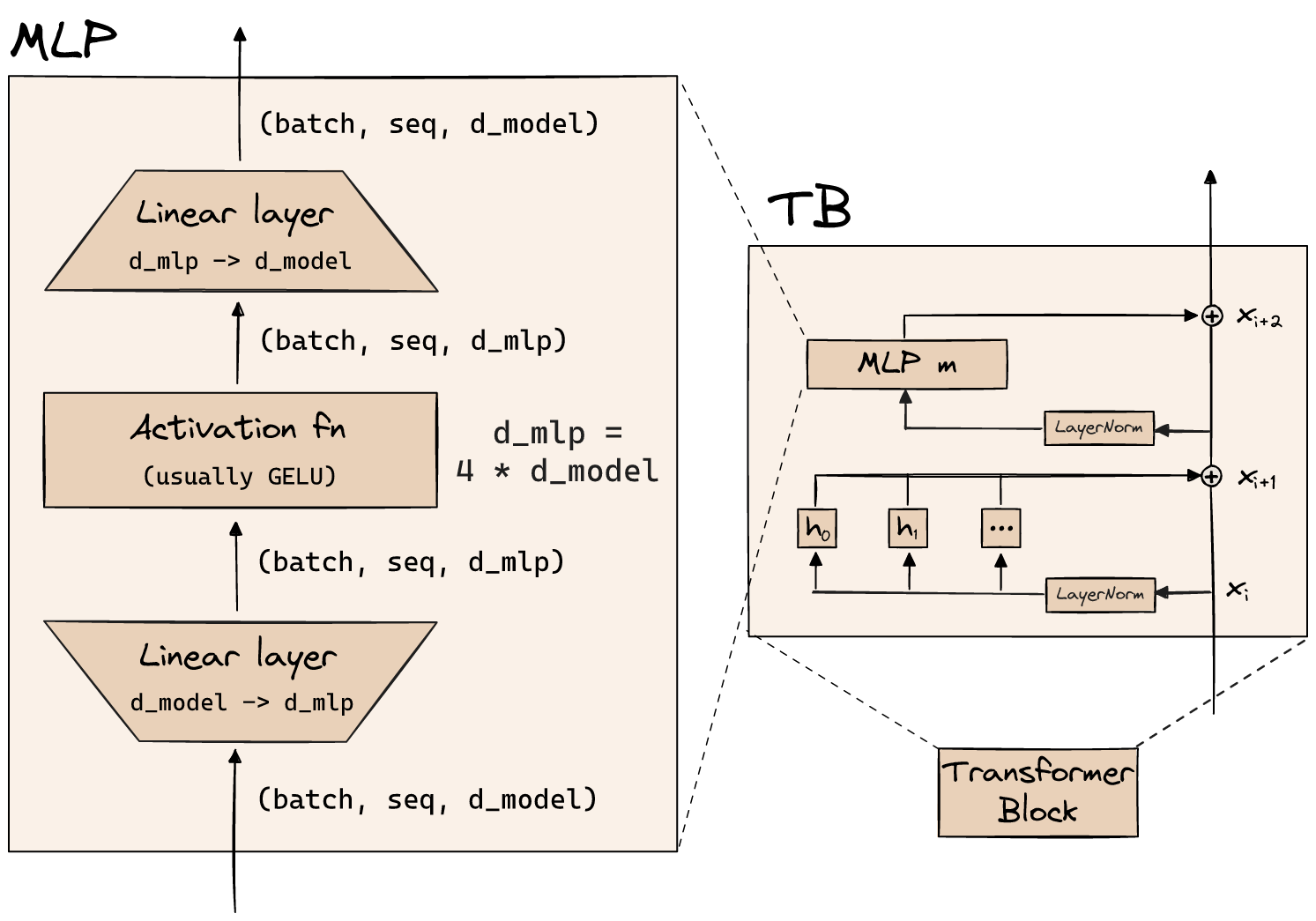Figure 3: The structure of the MLP layer in a Transformer block (from Arena)

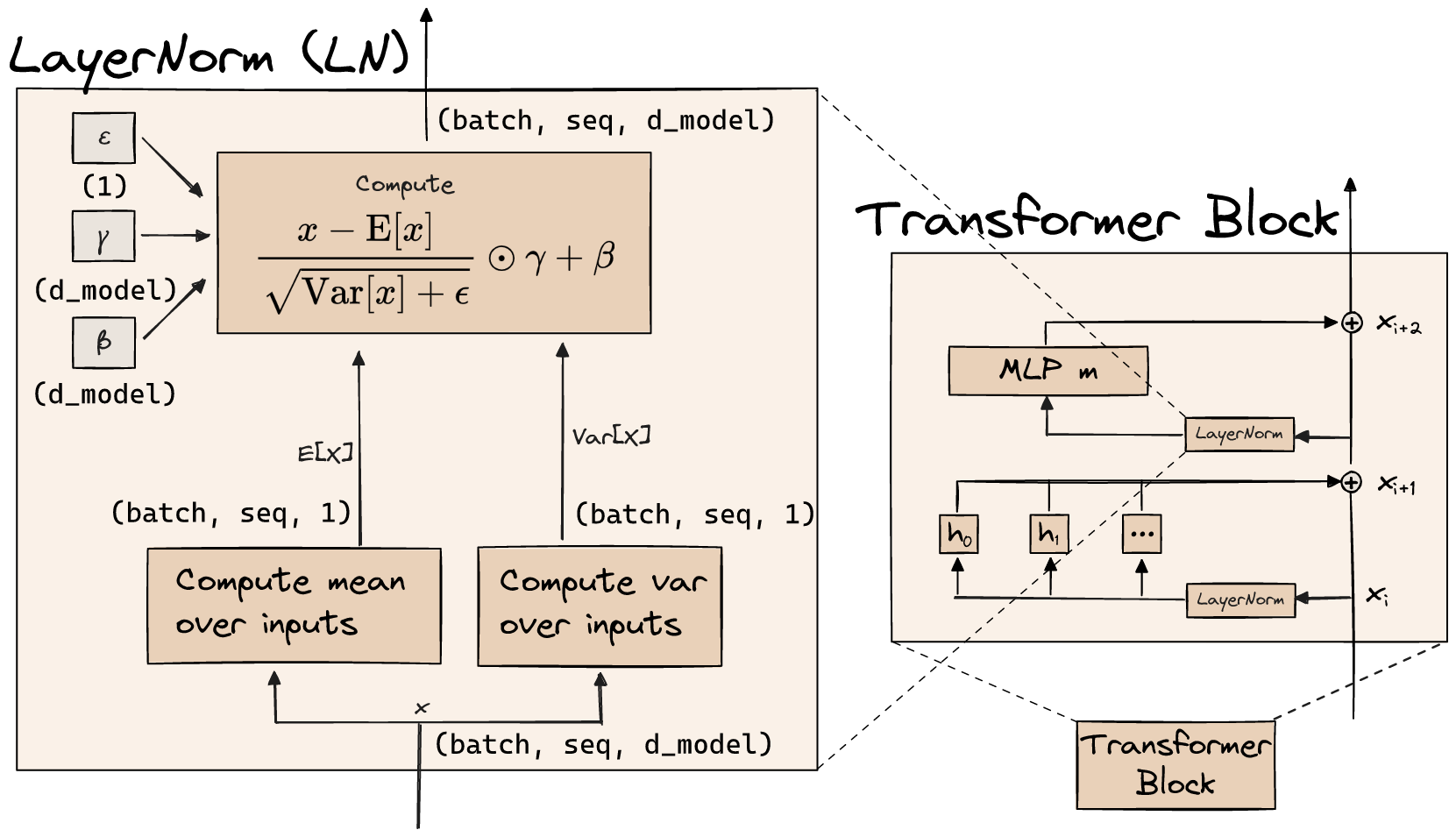Figure 4: The structure of the layer normalization in a Transformer block (from Arena)

Basic ideas and research topics

In this section, I’m gonna explain some terms for mech interp and help you understand the basic ideas of doing mech interp research. I’ll try to make it easy!

Note that I’ll only introduce something that I think is important. If you wanna learn more about the concepts in mech interp, please refer to: A Comprehensive Mechanistic Interpretability Explainer & Glossary which is a very comprehensive guide for beginners that I strongly recommend!

Important concepts

Features
There are a lot of definitions for features. Unfortunately none of the definitions above can be widely recognized, so it’s open for anyone who wants to seek for the essence of the features. Generally speaking, a feature is a property of an input which is interpretable or cannot be understand by humans. Practically speaking, a feature could be an activation value of a hidden state in a model (at least lots of work is focusing on this).

How to find a feature? Or how to know that the thing you find is likely to be a feature? Here I want to quote the concept of “the signal of structure” proposed by Chris Olah in the post of his thoughts on qualitative research:

  The signal of structure is any structure in one’s qualitative observations which cannot be an artifact of measurement or have come from another source, but instead must reflect some kind of structure in the object of inquiry, even if we don’t understand it.

Just like the discovery of cells under a microscope. The shape of the cells cannot be random noise but strong evidence for the structure of them.

Circuits
If we view a language model as a directed acyclic graph (DAG) $M$ where nodes are terms in its forward pass (neurons, attention heads, embeddings, etc.) and edges are the interactions between those terms (residual connections, attention, projections, etc.), a circuit $C$ is a subgraph of $M$ responsible for some behavior. That means the components inside the circuit have a big influence on the output of the task, while the components outside the subgraph have almost no influence.

From my perspective, a circuit is a path from an input to an output, just like the way between two hosts in the routing networks.

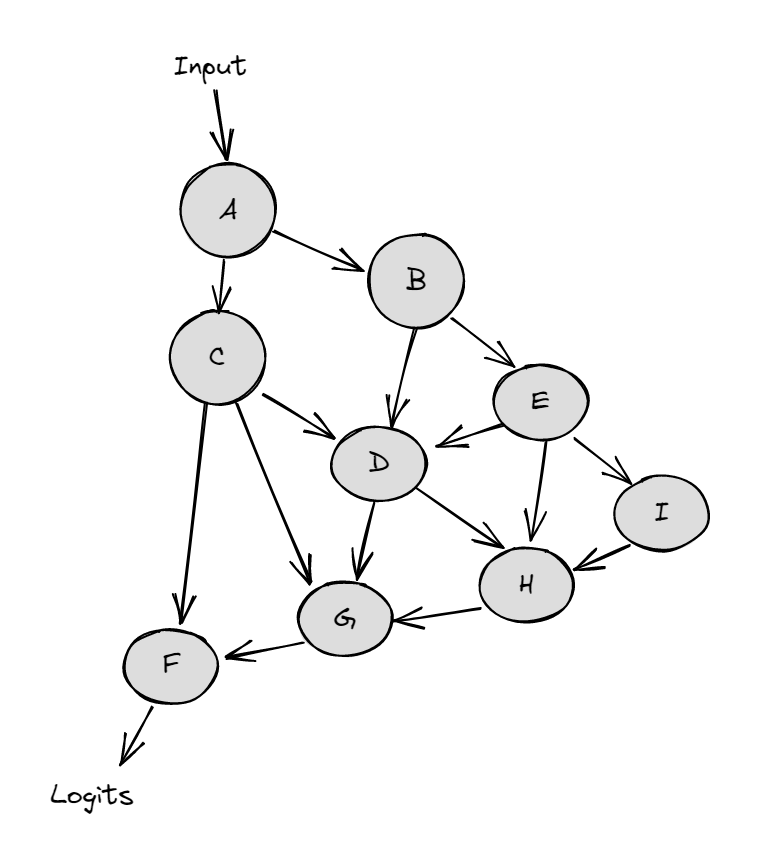Figure 5: The computational graph of a model (from Arena)

Superposition
Superposition is a hypothesis that models can represent more features than the dimensions they have.

Ideally we expect that each neuron only corresponds to one feature, so we can investigate or even control the feature using the neuron reserved for it. But in practice we find that a neuron fires for more than one features, which is called the phenomenon of polysemanticity in neurons. We believe that we have more features than model dimensions, so we can also say that more than one neurons fire when a feature appears. That is to say, there is not a one-to-one correspondence between neurons and features.

Privileged basis
It’s a weird idea that I have some doubt on it (maybe I haven’t grasp the core idea of it…).

My understanding: There are many vector spaces in a model, for example, the residual stream in a layer, the output of the ReLU in a MLP layer, etc. Each vector space can be seen as a representation. Given an input, we can get the hidden states in different vector spaces during the forward propagation of the model. If we could view neurons as directions which may correspond to features in a vector space, then we say there is a privileged basis in this vector space. That is to say, each value at a specific dimension is aligned with a neuron, and that value may be a interpretable feature (maybe not).

Not all vector spaces in a model have privileged basis. The most accepted view is that privileged bases exist in attention patterns and MLP activations, but not in residual streams. A general law is that a privilege basis often appears with a elementwise nonlinear operation, for instance, ReLu, Softmax, etc. If the operations around a representation are all linear, then we say the basis in the representation is non-privileged. For example, the operations around a residual stream are often non-linear (e.g. $W_{in}$ and $W_{out}$ of a MLP layer which correspond to the “read” and “write” operation on the residual stream). If we apply a rotation matrix to the original operations to change the basis, then the result will be unchanged because In other words, something is a privileged basis if it is not rotation-independent, i.e. the nature of computation done on it means that the basis directions have some special significance. A privileged basis is a meaningful basis for a vector space. That is, the coordinates in that basis have some meaning, that coordinates in an arbitrary basis do not have. It does not, necessarily, mean that this is an interpretable basis.
a space can have an interpretable basis without having a privileged basis. In order to be privileged, a basis needs to be interpretable a priori - i.e. we can predict it solely from the structure of the network architecture.

Research techniques

Circuits Discovery
Finding the circuit for a specific task attracts the attention of lots of researchers. The thing we wanna do is to get the relevant components for a specific task. A naive idea is to test the components one by one using causal intervention: change the value of one component while keeping others unchanged, and check if it influences the output. This technique is also called ablation or knockout.

To achieve this, we have two possible ways: denoising (find useful components) and noising (delete unuseful components). We usually prepare a clean prompt which is relevant to the task (results in a correct answer) and a corrupted prompt which has nothing to do with the task. Before finding circuits, the two prompts are fed into the model separately to get a clean run and a corrupted run.

If we use denoising, at each step we replace (patch) the value of a component in the corrupted run with that in the clean run. If the output is closer to the correct answer under a specific metric (e.g. KL divergence or logit difference), then we add the component into the circuit. If we use noising, then we should replace a component in the clean run with that in the corrupted run. If the output is almost unchanged under a threshold, then we regard the component as useless and delete it. Generally speaking, denoising is better than noising. To understand this, I want to quote a line in Arena: noising tells you what is necessary, denoising tells you what is sufficient.
Several techniques in this area:

  • activation patching (aka causal mediation/interchange interventions…) A method for circuits discovery that take nodes into consideration.
  • path patching A variant of activation patching that also take edges into consideration to study which connections between components matter. For a pair of components A and B, we patch in the clean output of A, but only along paths that affect the input of component B. While in activation patching, all the subsequent components after A are affected.
  • attribution patching An approximation of activation patching using a first-order Taylor expansion on the metric. This method is used to speed up circuits finding.
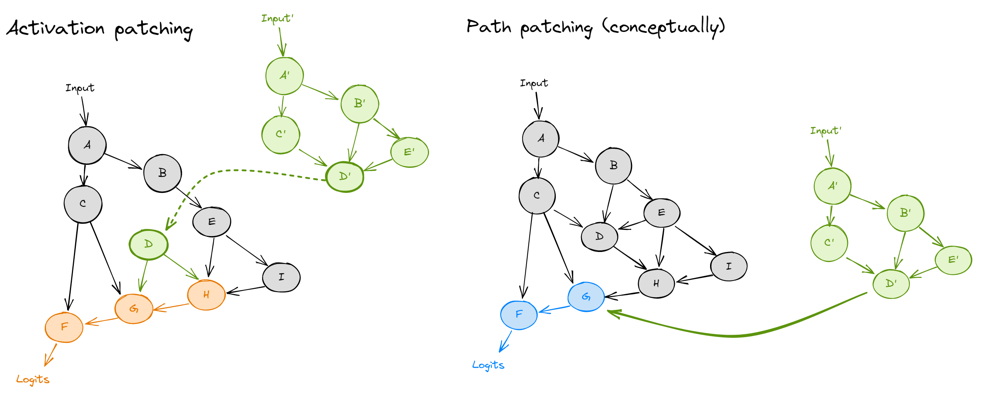Figure 6: Comparison of activation patching and path patching (from Arena)

The difference between activation patching and path patching are shown in Figure 6. In activation patching, we simply patch the node $D$ with $D’$, so the nodes after $D$ ($H, G$ and $F$) are affected. While in path patching, we patch edges rather than nodes. For example, we only want to patch the edge $D \to G$, which means the only change is the information from node $D$ to node $G$. As a result, only $G$ and $F$ are affected while $H$ isn’t.

Dictionary Learning
Dictionary Learning aims to deal with the problem of superposition. The idea is like compression sensing in the field of signal processing and is discussed in this article. The implementation of dictionary learning is to train a sparse autoencoder (SAE).

An autoencoder consists of an encoder and a decoder. The encoder receives an input and compresses it to a lower dimension, and the decoder maps the hidden representation to the original input. The goal of the autoencoder is to get the representation of the input while compressing it. The autoencoder is optimized using the reconstruction loss.

Compared with the autoencoedr, the dimension of the hidden representation in SAE is always higher than that of the input, which means the SAE does something completely opposite to the autoencoder. The idea behind is that the model dimension is smaller than the number of features to represent. The model may use superposition to make full use of limited neurons to represent more features. To get one-to-one correspondence between neurons and features, we map the representation to a higher dimensional vector space with SAE encoder. Once we get the representation in SAE (let’s call it sparse features), we maps it back to the original input with SAE decoder.

In practice, any hidden state in a model can be studied using SAE. For example, when we want to get the sparse features of the activations $h$ in a MLP layer. We can do as follows:

$$ z = ReLU(W_{enc}h + b_{enc}) $$ $$ h^{\prime} = W_{dec}z + b_{dec} $$

$$ loss = \mathbb{E}_{h}\left[||h-h^{\prime}||_{2}^{2} + \lambda||z||\right] $$

Note that $ h = [h_{1}, h_{2},…,h_{n}]^{T} \in \mathbb{R}^{n\times1} $ is a hidden state with $n$ dimensions, and each $h_{i} \in H$ is the value of a specific dimension $i$. $W_{enc} \in \mathbb{R}^{m\times n}$ maps the hidden state to a new vector space with dimension $m>n$, $W_{dec} \in \mathbb{R}^{n\times m}$ maps the sparse features back to the original shape, $ b_{enc} \in \mathbb{R}^{n} $ and $ b_{dec} \in \mathbb{R}^{n} $ are learned bias. The loss function consists of two parts: the MSE loss as the reconstruction loss and L1 norm with a coefficient $\lambda$ to encourage the sparsity of feature activations. It is the regularization term that separates SAE from ordinary autoencoders, so as to discourage superposition and encourage monosemanticity.

To better understanding the encoder and decoder in SAE, we can write a sparse feature $ f_{i} $ as an element of $ z $ :

$$ f_{i}(h) = z_{i} = ReLU(W^{enc}_{i,.}\cdot h + b^{enc}_{i}) $$

Each sparse feature $ f_{i} $ is calculated using row $i$ of the encoder weight matrix. As for decoder, we can write $ h^{\prime} $ as:

$$ h^{\prime} = \sum_{i=1}^{m}f_{i}(h) \cdot W^{dec}_{.,i} + b_{dec} $$

;The reconstructed activation $h^\prime$ can been seen as a linear addition of all the features. Each column of the decoder matrix corresponds to a feature, so we call it a “feature direction”. Note that sometimes the L1 norm term in the loss function can be replaced by $ \lambda\sum_{i=1}^{m}f_{i}(h)||W^{dec}_{.,i}||_{2} $ which places a constraint to the decoder weights to reduce ambiguity in the addition operation (we want only one or a few features to be large).

For simplicity, The details of the model structure, training method and evaluation will not be shown here.

Model Steering
A useful technique for eliciting certain model behaviors in a mechanistic way.

Research Areas

Figure 7: The route of mech interp (from transformer-circuits.pub/2024/july-update/)

Theory

  • Understand model components
  • Understand model behaviors

Application

  • interpretable model structure
  • AI alignment
    Avoid bias and harmful behaviors

Some Useful Resources

Here I list some resources that would be helpful for you to get started quickly in the field.

Tutorials

Frameworks and Libraries

  • TransformerLens  A library maintained by Bryce Meyer and created by Neel Nanda.
  • SAELens  Originates from TransformerLens, and is separated from it because of the popularity and importance of SAE.
  • CircuitsVis  A good tool for visualizing LLMs.
  • Plotly  A good tool for plotting.

Forums and Communities

Companies, Institutes, Labs and Programs

Blogs

Chris Olah  
Neel Nanda  
* Neel Nanda at the Alignment Forum
Arthur Conmy  
Andy Zou  
Jacob Steinhardt  
David Bau  
Max Tegmark  
Trenton Bricken  
Callum Mcdougall  
Alex Turner(TurnTrout)  
     

…